Skip to main content
Research and Practice in Technology Enhanced Learning
Research and Practice in Technology Enhanced Learning Cover Image
Download PDF

Relationship between interest and mathematics performance in a technology-enhanced learning context in Malaysia

Research and Practice in Technology Enhanced Learning volume 14, Article number: 21 (2019) Cite this article

Abstract

The primary aim of this preliminary study is to examine a possible association between interest and mathematics performance among Malaysian students in a technology-enhanced learning environment. The Mathematics Interest Inventory was administered to 40 students to measure students’ interest towards mathematics, while a mathematics test was used to measure students’ mathematics performance. Results of the descriptive statistical analyses revealed that the students were relatively interested in mathematics. Correlational analyses showed that interest was not significantly correlated to mathematics performance among the students. Nevertheless, a significant relationship between interest and mathematics performance was found among students who had lower mathematics performance. The findings of this study pointed to the importance of igniting interest among students with lower mathematics performance given its strong link to mathematics performance. The Interest-Driven Creator theory served as an anchor in the theoretical framework of the study and it was discussed within the context of mathematics learning.

Introduction

In Malaysia, mathematics is a compulsory subject for all primary and secondary school students. Over the years, Malaysia has participated in international assessments like Trends in International Mathematics and Science Study (TIMSS) and Program for International Student Assessment (PISA). In 1999, when Malaysia first participated in TIMSS, its eighth-grade students’ mathematics performance was above average with a mean score of 519, and Malaysia ranked 16th out of 38 countries (Ministry of Education Malaysia, 2013). However, over the following years, Malaysian eighth-graders’ mathematics achievement in TIMSS showed a declining trend whereby in TIMSS 2011, they attained a low mean score of 440 and Malaysia ranked 26th out of 45 countries (Ministry of Education Malaysia, 2013). Nevertheless, in TIMSS 2015 the mathematics score improved by 25 points to an overall score of 465 (Mullis, Martin, Foy, & Hooper, 2016). Malaysia was one of the 18 countries which had shown improved mathematics performance in TIMSS 2015 as compared to TIMSS 2011 (Ministry of Education Malaysia, 2017).

On the other hand, the results in PISA 2009 showed that nearly 60% of the 15-year-old Malaysian students who participated in the assessment were below the minimum benchmarks of mathematical literacy set by PISA, which is required to participate effectively and productively in life (Ministry of Education Malaysia, 2013). Later in PISA 2012, the mathematics performance was subpar again, and Malaysia was placed 52nd out of 65 participating countries, with a mean score of 421 that was below the OECD average (OECD, 2014). In brief, the findings from these international assessments suggest that there have been fluctuations in Malaysian students’ mathematics performance.

As widely believed, interest has a vital role in mathematics learning (Heinze, Reiss, & Franziska, 2005; Yu & Singh, 2016). Hidi and Renninger (2006) describe interest represents a psychological state of engaging or having the tendency to reengage in a particular content in the course of time; it was categorised into individual interest and situational interest. According to Ainley (2006), interest is defined as an affective state that refers to the subjective experience in learning. In this study, interest is operationally defined as students’ affective state of being engaged in mathematics learning whereby students enjoy the learning process. Heinze et al. (2005) carried out a study on 500 German students who were at the seventh grade and eighth grade to explore their mathematics achievement and interest as well as the association between the variables. The study concluded that interest towards mathematics learning could be considered as a predictor for mathematics achievement (Heinze et al., 2005). Sauer (2012) found that students’ interest towards learning is one of the contributing factors in successful academic performance. A study conducted on 511 secondary students in Nigeria showed that academic achievement and interest in learning are significantly correlated (Kpolovie, Joe, & Okoto, 2014). Also, Gilbert (2016) showed that students with a higher level of interest in mathematics had lower performance-avoidance goals for both types of mathematical tasks which required high and low cognitive processes. Moreover, Thien and Ong (2015) pointed out that mathematics anxiety and mathematics self-efficacy did affect Malaysian students’ mathematics performance while Pantziara and Philippou (2013) revealed that self-efficacy in mathematics can directly affect students’ interest in mathematics.

In contrast, Yu and Singh (2016) reported an unanticipated result which showed that the relationship between interest and mathematics performance was insignificant. The study adopted interest and self-efficacy as the motivational variables and concluded that teachers’ emotional support influenced students’ interest in mathematics. Yu and Singh (2016) explained that interest might not be a direct predictor of mathematics performance, and it could be due to the reciprocal effects with personal variables (i.e. self-efficacy or self-regulations) or school-related variables (i.e. classroom practices). In a related vein, Thien and Ong (2015) highlighted that in PISA 2012, unlike affective variables like mathematics self-efficacy and anxiety, mathematical interest did not significantly relate to Malaysian students’ mathematics performance. In view of these inconclusive findings, this study intended to investigate the relationship between interest and mathematics performance among Malaysian students in a technology-enhanced learning environment.

Theoretical framework: Interest-Driven Creator (IDC) theory in learning mathematics

Many studies have put effort in intervening an approach to promote and develop students’ interest in mathematics learning. The IDC theory suggests that students can be nurtured as creators after they have engaged in interest-driven learning activities regularly with technology support (Chan et al., 2018). There are three anchored concepts in the IDC theory, namely, interest, creation, and habit, whereas each of them will go through to a continuum learning activity that subsequently forms a loop (Chan et al., 2018).

Firstly, the interest loop comprises three coherent components which are triggering interest, immersing interest, and extending interest (Wong, Chan, Chen, King, & Wong, 2015). In the IDC theory, stimulating curiosity is one of the processes in triggering situational interest; however, presenting attractive learning subject matters is inadequate for this purpose. To provoke situational interest, teachers or instructional designers should scaffold knowledge deficit, which subsequently can help students be immersed or fully engaged in the learning process by providing optimum levels of challenging learning tasks. As for the final component in the interest loop, it explains that utility implications of the learning content are crucial for sustaining students’ interest (Wong et al., 2015). In relation to mathematics learning, students’ interest can be promoted by firstly presenting a mathematical problem that is able to provoke and confront students’ prior knowledge, and scaffold students to tackle challenges that help students gain successful experiences and finally present the practical value of the learning content.

Next in the creation loop, there are three components which are imitating, combining, and staging (Chan et al., 2018). According to Chan, Looi, and Chang (2015), the early stage of learning process includes imitation from a model, as an attempt to understand the model’s ideas, methods, or ways of doing things. Then, students will choose what to retain or remove, and come up with their own interpretation or ideas as a result of ‘combination’. To complete the creation process, students should be provided with a platform to present their product (Chan et al., 2015). In the context of mathematics learning, the creation loop can be operationalised as simply as a mathematics problem-solving situation in a classroom. Mathematics teachers usually demonstrate a step-by-step method to approach a mathematics question, and in return, students are asked to imitate the process for a similar question. When students are able to solve the question on their own, it can be known as a completed ‘combination’ process as they have acquired the skills and knowledge to answer a mathematics question. Staging can be as straightforward as showing their working solution on the board in the classroom to their peers.

Finally, the habit loop consists of three components: cueing environment, routine, and satisfaction (Chen et al., 2015). In the view of the IDC theory, it is important and possible to develop a positive learning habit to nurture a lifelong interest-driven creator (Chen et al., 2015). Although the habit formation process takes time and is highly related to students’ affective characteristics and cognitive behaviours, teachers should begin with easy and simple habits; therefore, it comes down to the question of what is the learning habit teachers would like students to form (Chen et al., 2015). Regarding learning mathematics, there are a few fundamental and important learning habits like memorisation of the multiplication table, the accurate and systematic way of writing mathematics equation, or an analytic approach in solving mathematics questions. In the process of developing students’ interest towards mathematics, it is inevitable that students are required to be innately involved in solving a mathematics problem regularly, and that is when habits comes into play, to help them be comfortable, familiar, and most importantly, answer a mathematics question correctly as guided by the teacher. In the long term, as conceptualised in the IDC theory, students’ satisfaction towards learning can be increased with increasing successful experiences (Chan et al., 2018; Chen et al., 2015).

When taken together, from the IDC theory perspective, nurturing interest in learning mathematics includes provoking students’ interest with scaffolding mathematics problems, guiding students to tackle the challenges, providing utility value of the learning content, enabling students to imitate the approach of solving a mathematics question, allowing them to answer on their own and presenting it to teacher or peers, and lastly, guiding students to form fundamental habit in arithmetic learning process in every step of the way. It would be reasonable to assume that the aforesaid discussion provides a glimpse of how the IDC theory can be applied to guide the design of learning activities in mathematics. The potential of the IDC theory is far-reaching but more studies need to be carried out to validate its application in the learning context across various disciplines.

It is believed that interest has a vital role in students’ learning performance (Gilbert, 2016; Heinze et al., 2005; Kpolovie et al., 2014; Sauer, 2012). However, interest may not be a direct predictor of mathematics performance (Yu & Singh, 2016) and may not significantly relate to Malaysian students’ mathematics performance after factoring in the results from PISA 2012 (Thien & Ong, 2015). Therefore, this preliminary study leveraged on the IDC theory to understand more about the relationship between interest and students’ mathematics performance in the Malaysian context.

Objective of the study

The objective of the study is to explore the association between interest and mathematics performance among Malaysian students in a technology-enhanced learning environment from the perspective of the IDC theory. Specifically, the following research questions will be answered:

  1. 1.

    What is Malaysian students’ interest profile towards mathematics in a technology-enhanced learning environment?

  2. 2.

    Is there any relationship between interest and mathematics performance among Malaysian students in a technology-enhanced learning context?

Description of the instructional context

The mathematics instructions aim to achieve two learning objectives under the topic of Loci in Two Dimensions, which is Chapter 9 in Form Two (Grade 8) mathematics syllabus (Ministry of Education Malaysia, 2002). The topic was chosen in this study because nearly 43% of the topics in mathematics syllabus for secondary education in Malaysia are related to geometry (Ministry of Education Malaysia, 2004). There are two learning objectives under this topic which are to (1) understand the concept of two-dimensional loci and (2) understand the concept of the intersection of two loci.

Geometer’s Sketchpad (GSP) was used as a supporting tool in this study. It is a dynamic geometry software that can be used to create, explore, and analyse a broad range of mathematical concepts such as geometry, algebra, calculus, and trigonometry (Steketee, Jackiw, & Chanan, 2001). In this study, GSP was utilised to demonstrate the concept of loci by showing the points moving according to the mathematically defined conditions. As per the learning objectives of the topic, there were four types of loci in different conditions, and hence GSP was used to explain the concept for every condition.

In relation to the interest component of the IDC theory, in order to stimulate curiosity and challenge students intellectually to stimulate interest in the learning topic, students were asked to answer the question, ‘Do you think that every passenger in every capsule of the London Eye will be seeing the same view of London, after they have completed the Ferris wheel ride?’. The question is meant for students to reason why every capsule is moving at the same path, which will be related to the definition of locus whereby it is the pathway of moving points under a certain condition (e.g. every capsule is moving at a constant distance from the centre of London Eye). An example of the GSP teaching material is included in Appendix 1.

For the creation process, the mathematics instructions were structured in a way that students could observe how teachers construct locus for every specific condition. The teacher used the opportunity to emphasise the importance of using the correct mathematical tool (i.e. compass and ruler) to construct an accurate geometrical figure. When students were able to imitate the process to construct the correct locus for certain conditions, it is known as a complete ‘combination’ process as they have acquired the skills to approach the questions under these learning objectives.

The habit in the mathematics learning process is important to facilitate mathematical understanding in the long term. For this reason, it is critically important to draw an accurate geometrical figure with correct tools (teachers relate the importance to the nature of work of an architect). Therefore, to form the habit of constructing accurate figures, students were asked to use a ruler to draw straight lines and use a compass to draw a circle and the right steps to draw a perpendicular line and angle bisector.

Methods

This is a correlational research whereby the association between two variables was investigated. A questionnaire and a mathematics test were administrated to measure interest and mathematics performance, respectively. The Mathematics Interest Inventory (MII) comprising 27 items which was originally developed by Stevens and Olivárez (2005) is used to measure students’ interest towards mathematics. MII is a seven-point scale, ranging from 1 = not at all true of me to 7 = very true of me, which was used for all items in this instrument. There are 11 reversed items in the instrument, specifically items 11 to 20 and item 26. These negatively stated items were reverse-scored before the scores were computed at the data analysis stage.

Mathematics performance is measured by a mathematics test that questions on the topic of Loci in Two Dimensions, which is Chapter 9 in the Form Two (Grade 8) mathematics syllabus (Ministry of Education Malaysia, 2002). The mathematics test comprises six questions with a total minimum score of zero and a maximum score of 20. Nine periods of mathematics lessons were used for this study (30 min for each period). The first seven periods were used for mathematics instructions and the last two periods were for administration of the MII and mathematics test.

The content validity of the instruments was established through a panel of expert comprising a mathematics lecturer, an educational psychologist, and an expert in the field of educational technology. All of the experts were lecturers in public universities in Malaysia. The experts identified and modified double- and multiple-barrel items, and they recommended modifications to some words and phrases of the items in order to align them to the objectives of this study. Modifications to the items were made with the written permission from the respective authors. The reliability of the MII was established with Cronbach’s alpha value at .82 which is categorised as highly reliable according to Cohen, Manion, and Morrison (2007).

The 40 participants in this study were from two intact classrooms from two national public secondary schools in Selangor state, Malaysia. Geometer’s Sketchpad (GSP) was used in both classrooms to demonstrate the concept of locus to achieve the learning objectives. GSP is a dynamic geometry software that can be used to create, explore, and analyse a broad range of mathematical concepts such as geometry, algebra, calculus, and trigonometry (Jackiw, 1991).

Results and findings

Students’ interest profile towards mathematics in a technology-enhanced learning context

Interest towards mathematics was measured among the 40 students, and the interest mean score is 4.70 with a standard deviation of 0.64. The mean score is only slightly higher than the mid-point of the scale (4.0) which represents the neutral interest disposition. The mean score suggests that the students were in between ‘not sure’ and ‘somewhat true of me’ in accordance with interest disposition towards mathematics. This suggests students are inclined to have a positive disposition towards learning mathematics.

Table 1 presents students’ interest towards mathematics. With regards to the items related to positive valence, i.e. item one until ten, the majority of them agreed the descriptors were very true of them. Among others, for the descriptor ‘I want to know all about how to do mathematics problems’, 45% of the respondents agreed that this is very true of them, 42.5% agreed that it is very true that knowing a lot about mathematics is helpful, and the same percentage of them choose to work on mathematics.

Table 1 Students' interest towards mathematics
Full size table

With regards to negative experience related to mathematics which includes being cognitively challenged by mathematics and thus choosing to avoid it, majority of the respondents were not sure about it. For instance, 37.5% of them were not sure if they want to stop and start working on something else when they are working on mathematics. There are one-fourth of them who were not sure, but 20% thought that it is somewhat true that they get mad easily when working on mathematics. It is notable that there were 37.5%, 17.5%, and 7.5% of the respondents who agreed they are wasting time on mathematics at the levels of very true, true, and somewhat true of them, respectively.

Relationship between interest and mathematics performance

The relationship between interest and mathematics performance was explored using the Pearson product-moment correlation coefficient. The rule of thumb by Cohen et al. (2007) was used for interpreting the results of r values in this study. No significant relationship was established between interest and mathematics performance for the 40 students, at r = 0.24 with p = 0.14. The strength of the relationship was considered as small (Cohen et al., 2007), and there was not much overlap between the two variables as only 5.7% of variances were shared between them. It should be noted that the mean score of their mathematics performance is 9.08 out of 20 (SD = 3.88) and this indicates that the students did not pass the mathematics test as a whole.

To further investigate the association between interest and mathematics performance, students were divided into two groups with different levels of mathematics performance. The first group (group 1, n = 20, higher mathematics performance) had a mean score of 10.73 (SD = 3.87) for mathematics performance which was considered as a pass. Group 1 had a mean score of 4.61 (SD = 0.47) for interest. On the other hand, the second group (group 2, n = 20, lower level of mathematics performance) had a mean score of 7.43 (SD = 3.20) for mathematics performance which was considered as a fail. Group 2 had a mean score of 4.78 (SD = 0.77) for interest. The results indicate that students in group 2 with lower mathematics competency had a slightly higher level of interest compared to that of students in group 1 with higher mathematics competency.

With regard to the higher mathematics performance group, there was no significant relationship between interest and mathematics performance at r = 0.12 with p = 0.62. There was only 1.4% of shared variances between the two variables for this group of students. In contrast, the lower mathematics performance group established a significant relationship between interest and mathematics performance at r = 0.52 with p < 0.05. According to Cohen et al. (2007), the strength of the significant relationship was large with 27.04% shared variance. This suggests that interest towards mathematics helps to explain approximately 27% of the variance in this particular group of students’ mathematics performance.

Discussion and conclusion

The aim of this study is to examine the association between interest and mathematics performance in a technology-enhanced learning environment among Malaysian students in Form 2 (Grade 8). Students were inclined to like mathematics but at the same time did not quite see the benefits of learning the subject. In other words, students understood the importance and practical implication of mathematics subject but seemed to perceive learning mathematics as unnecessary. In relation to the relatively low mathematics test scores, it seems possible that these results were due to students’ frustration and helplessness while answering the test questions could have been challenging to them. This result is similar to that of PISA 2012 in which Malaysian students had significantly higher levels of instrumental motivation and mathematical interest compared to OECD average but had a higher level of mathematics anxiety than OECD average too (OECD, 2014; Thien & Ong, 2015). One possible reason for this is that students could be feeling anxious about mathematics while being well aware of its utility value in the Malaysian education context. This is because they will need to gain a pass in general mathematics in order to gain admission to many institutions of higher learning.

The findings of the present study indicate that interest is not significantly related to mathematics performance in general, especially among those with higher mathematics performance. However, interest towards learning mathematics has a significant positive relationship with mathematics performance for those with low mathematics performance. These results reflect those of Köller and Baumert (2001) in which relationship between academic interest and mathematics achievement is weaker when learning activities are driven by extrinsic values like wanting to get good grades in the examination or avoiding negative consequences from not performing well. It was argued that interest becomes a more critical antecedent of mathematics performance when the instruction is not highly structured (Köller & Baumert, 2001). Yu and Singh (2016) argued the reciprocal effects like personal variables (self-efficacy) and classroom practice may be the reasons that interest is not a direct predictor of mathematics performance. In relation to this study, a possible explanation for this is that students who were in the high mathematics performance group were driven to learn for extrinsic reasons and their mathematics learning activities in the classroom probably were more structured as they have better mathematics competency, and hence, despite having lower level of interest towards mathematics, they could still perform better in mathematics test. When seen through the lens of the IDC theory, interest towards mathematics of this higher performance group of students can be developed by scaffolding the knowledge deficit and explaining the utility implications of the learning content to sustain their interest towards the learning content.

On the other hand, students who were weaker in mathematics had more interest in the subject as compared to those who were better in mathematics. Findings of the present study are in line with those of PISA 2012 where Malaysian students had higher than OECD average level of mathematics interest, but the mean scores for mathematics performance were lower than OECD average (OECD, 2014; Thien & Ong, 2015). In the context of the IDC theory, this group of students probably have interest towards mathematics but requires more help at the creation stage where students have to analyse, evaluate, and create in the ‘combining’ stage (Chan et al., 2018). It may be that this group of students requires more help in ‘imitating’ where a spectrum of learning activities needs to be given to guide students to remember, understand, and apply the demonstrated mathematics problem-solving methods (Chan et al., 2015). For instance, this group of students might need more time to internalise the steps to construct a locus for certain conditions. This means that the teacher probably needs to facilitate more frequently than usual for the step-by-step demonstration of constructing an accurate locus.

As stipulated in the creation loop of the IDC theory (Chan et al., 2015), students were not able to progress towards creating their version of understanding of teacher’s demonstration in learning mathematics, if they have not fully made sense of the inputting information from their model, i.e. mathematics teacher. In the same vein, it should not be neglected that it is a primary priority for students to develop interest as imposed in the interest loop (Wong et al., 2015), before they can be facilitated for creation process in learning mathematics, especially for students with low mastery level of mathematics. This could be achieved by stimulating curiosity through presenting knowledge deficit with mathematics problems, allowing students to tackle the problems, and presenting practicality of the learning content. Subsequently, as described in the habit loop (Chen et al., 2015), these learning activities have to be conducted regularly in order to nurture an interest-driven mathematics learner while fundamental habit in learning mathematics could be formed in the process too.

In conclusion, this study, though preliminary in nature, it would be reasonable to assume that the students who participated in this study were relatively interested in mathematics although it appeared that their interest in mathematics may have been driven by the examination grades. However, the link between interest and mathematics performance was weak for those who had a higher level of performance in mathematics but stronger for those with lower mathematics performance. Obviously, more needs to be done by teachers to spark the interest among students who were weaker in mastering mathematics given its significant relationship with mathematics performance. Thereafter, students should be exposed to a broad range of learning activities regularly in order to allow them to imitate problem-solving skills in mathematics from their teachers, and such repetitive behaviours will hopefully translate into learning mathematics habits. At this point in time, it can only be speculated that the IDC theory may have a bigger impact on lower mathematics achievers than higher achievers when applied into the learning designs of learning activities.

Limitations of the study

This preliminary study has several limitations. Given that it was our first attempt to apply the IDC theory into the mathematics learning activities, more work needs to be done to concretise the instructional design of the activities. The IDC theory was primarily used to explain the exploration on the relationship between mathematics interest and mathematics performance in this study. The data of interest in this study were collected through questionnaires alone. It was based entirely on students’ honesty and how they perceived their interest disposition towards mathematics. It also must be recognised that only two classes of Form 2 (Grade 8) students from two different public secondary schools in the state of Selangor, Malaysia, were included in the study. As such, the results from this study cannot be generalised beyond this group of students.

In addition, other variables or factors that were not considered in the current analysis that could have been impactful include students’ prior knowledge on the learning topic, gender, and previous mathematics learning experience and performance. It is important to point out that the causal implications between interest towards mathematics learning and mathematics performance cannot be established as the correlational analysis does not reveal the causal effect among variables.

Suffice to say, this study has contributed in some ways to the current articulation of the IDC theory as seen from the Malaysian perspective given ‘that there is a symbiosis between theory and practice, and, for educational research, they cannot flourish without each other, even though they may have difficulty in living both with and without each other’ (Morrison & van der Werf, 2012, p. 399). We hope that the essence of the relationship between the IDC theory and the findings of this study will solidify the tenets of the theory and move it forward for better understanding and development in the community.

Availability of data and materials

Availability of data and materials upon reasonable requests.

Abbreviations

GSP:

Geometer’s Sketchpad

IDC:

Interest-Driven Creator

MII:

Mathematics Interest Inventory

OECD:

Organisation for Economic Co-operation and Development

PISA:

Program for International Students Assessment

SD:

Standard deviation

TIMSS:

Trends in International Mathematics and Science Study

References

  1. Ainley, M. (2006). Connecting with learning: Motivation, affect and cognition in interest processes. Educational Psychology Review, 18, 391–405. https://doi.org/10.1007/s10648-006-9033-0.

    Article  Google Scholar 

  2. Chan, T., Looi, C. K., Chen, W., Wong, L., Chang, B., Liao, C. C., . . . Ogata, H. (2018). Interest-driven creator theory: Towards a theory of learning design for Asia in the twenty-first century. Journal of Computers in Education, 5(4), 435-461.

    Article  Google Scholar 

  3. Chan, T.-W., Looi, C. K., & Chang, B. (2015). The IDC theory: Creation and the creation loop. Workshop Proceedings of the 23rd International Conference on Computers in Education, 814-820.

  4. Chen, W., Chan, T., Liao, C. C., Cheng, H. N., So, H., & Gu, X. (2015). The IDC theory: Habit and the habit loop. Worshop Proceedings of the 23rd International Conference on Computers in Education, 821-828.

  5. Cohen, L., Manion, L., & Morrison, K. (2007). Research methods in education (6th ed.). London: Routledge.

  6. Gilbert, M. C. (2016). Relating aspects of motivation to facets of mathematical competence varying in cognitive demand. The Journal of Educational Research, 109(6), 647–657. https://doi.org/10.1080/00220671.2015.1020912.

    Article  Google Scholar 

  7. Heinze, A., Reiss, K., & Franziska, R. (2005). Mathematics achievement and interest in mathematics from a differential perspective. Zentralblatt fuur Didaktik der Mathematik, 37(3), 212–220. https://doi.org/10.1007/s11858-005-0011-7.

    Article  Google Scholar 

  8. Hidi, S., & Renninger, K. A. (2006). The four-phase model of interest development. Educational Psychologist, 41(2), 111–127. https://doi.org/10.1207/s15326985ep4102_4.

    Article  Google Scholar 

  9. Jackiw, N. (1991). The Geometer’s Sketchpad [Computer software]. Emeryville, CA: Key Curriculum Press.

    Google Scholar 

  10. Köller, O., & Baumert, J. (2001). Does interest matter? The relationship between academic interest and achievement in mathematics. Journal for Research in Mathematics Education, 32(5), 448–470.

    Article  Google Scholar 

  11. Kpolovie, P. J., Joe, A. I., & Okoto, T. (2014). Academic achievement prediction: Role of interest in learning and attitude towards school. International Journal of Humanities Social Sciences and Education, 1(11), 73–100.

    Google Scholar 

  12. Ministry of Education Malaysia. (2002). Integrated curriculum for secondary schools: Form 2 Mathematics. Putrajaya: Curriculum Development Centre.

    Google Scholar 

  13. Ministry of Education Malaysia. (2004). Integrated curriculum for secondary schools: Syllabus mathematics. Ministry of Education Malaysia: Curriculum Developmenet Centre.

    Google Scholar 

  14. Ministry of Education Malaysia. (2013). Malaysia Education Blueprint 2013-2025: Preschool to post-secondary education. Putrajaya: Ministry of Education Malaysia.

    Google Scholar 

  15. Ministry of Education Malaysia. (2016). PISA 2015: Programme for International Assessment. Putrajaya: Ministry of Education Malaysia.

    Google Scholar 

  16. Ministry of Education Malaysia. (2017). Malaysia education blueprint 2013-2025: Annual report 2016. Putrajaya: Ministry of Education Malaysia.

    Google Scholar 

  17. Morrison, K., & van der Werf, G. (2012). Editorial. Educational Research and Evaluation, 18(5), 399–401.

    Article  Google Scholar 

  18. Mullis, I. V., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International results in mathematics. Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College.

  19. OECD. (2013). PISA 2012 Results: Ready to learn: Students' engagement, drive and self-beliefs,Volume III: OECD.

  20. OECD. (2014). In PISA 2012 results: What students know and can do- Student performance in mathematics, reading and science (Revised ed., Vol. 1). OECD Publishing. https://doi.org/10.1787/9789264208780.

  21. Pantziara, M., & Philippou, G. N. (2013). Students’ motivation in the mathematics classrooms: Revealing causes and consequences. International Journal of Science and Mathematics Education, 13, 385–411. https://doi.org/10.1007/s10763-013-9502-0.

    Article  Google Scholar 

  22. Sauer, K. (2012). The impact of student interest and instructor effectiveness on student performance. St. John Fisher College: Education Masters Retrieved from https://fisherpub.sjfc.edu/cgi/viewcontent.cgi?article=1244&context=education_ETD_masters.

    Google Scholar 

  23. Steketee, S., Jackiw, N., & Chanan, S. (2001). Geometer’s Sketchpad Reference Manual. Emeryville: Key Curriculum Press.

    Google Scholar 

  24. Stevens, T., & Olivárez, A. J. (2005). Development and evaluation of the mathematics interest inventory. Measurement and Evaluation in Counseling and Development, 38(3), 141–152.

    Article  Google Scholar 

  25. Thien, L. M., & Ong, M. Y. (2015). Malaysian and Singaporean students’ affective characteristics and mathematics performance: Evidence from 2012. SpringerPlus, 4, 563–577. https://doi.org/10.1186/s40064-015-1358-z.

  26. Wong, L., Chan, T., Chen, Z., King, R. B., & Wong, S. L. (2015). The IDC theory: Interest and the interest loop. In Workshop Proceedings of the 23rd International Conference on Computers in Education (pp. 804–813).

    Google Scholar 

  27. Yu, R., & Singh, K. (2016). Teacher support, instructional practices, student motivation, and mathematics achievement in high school. The Journal of Educational Research, 1–14. https://doi.org/10.1080/00220671.2016.1204260.

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the Research Management Centre of Universiti Putra Malaysia for funding this project (GP-IPS/2017/9540000).

Funding

This work was financially supported by the Putra Grant-Putra Graduate Initiative (IPS) under Research Management Centre, Universiti Putra Malaysia (Project number: GP-IPS/2017/9540000).

Author information

Affiliations

  1. Department of Science and Technical Education, Faculty of Educational Studies, Universiti Putra Malaysia, Serdang, 43400, Seri Kembangan, Selangor, Malaysia

    Shu Ling Wong & Su Luan Wong

Authors
  1. Shu Ling Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Su Luan Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

ShLW planned and implemented the study in close collaboration with Prof. SuLW. ShLW collected and analysed the data and collaborated in interpretation of results with Prof. SuLW. ShLW drafted the manuscript. Prof. SuLW edited the manuscript. Both authors revised the draft in all stages of finalisation. Both authors read and approved the final manuscript.

Authors’ information

Wong Shu Ling recently graduated from Universiti Putra Malaysia with a Master of Science degree in Educational Technology in 2019. She is currently a doctoral student at the Faculty of Education, University of Cambridge. Dr. Wong Su Luan is a professor at the Department of Science and Technical Education, Faculty of Educational Studies, Universiti Putra Malaysia.

Corresponding author

Correspondence to Su Luan Wong.

Ethics declarations

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix 1

Appendix 1

  • One of the section of GSP materials used in the mathematics instruction. The same version is available in Malay language too.

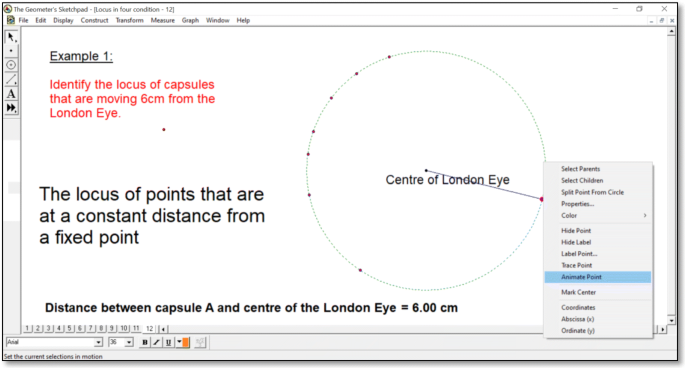
    figurea

  • ‘Animate point’ was clicked to show the movement of capsule A which illustrates the definition of a locus where it is the pathway of moving points under a certain condition.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Wong, S.L., Wong, S.L. Relationship between interest and mathematics performance in a technology-enhanced learning context in Malaysia. RPTEL 14, 21 (2019). https://doi.org/10.1186/s41039-019-0114-3

Download citation

Keywords

  • Interest-Driven Creator theory
  • Interest
  • Mathematics performance
  • Technology-enhanced learning